Sporenmessung - genau genommen
Liebe Pilzfreunde,
Ich habe hier einmal die Problematik der Sporenmessung näher beleuchtet - da dieses Thema erstens gut zu einem aktuellen Problemfall einer Hebeloma-Bestimmung passt und zweitens, dass ich die PNs die ich dazu bekommen habe damit einigermaßen beantworten kann. Per PN war diese Erklärung wie wir gleich sehen nicht so umfangreich machbar.
Für die Profis unter Euch: Bitte entschuldigt die oft dilettantische mathematische Ausdrucksweise - ich habe versucht es "verständlich" zu schreiben und Fachausdrücke versucht zu vermeiden. Vielleicht kann der ein oder andere Mathe-Profi dazu noch etwas mehr beitragen als ich, da ich ja nur ein praktischer Anwender der ganzen Rechnerei bin.
Los geht's...
Vielleicht hat sich der ein oder andere genau wie ich schon mal gefragt wie man Sporen eigentlich "richtig" misst.
Hier meine ich nicht die Technik der Messens an sich, auch nicht das Präparieren, Kalibrieren und das Mikroskopieren, sondern das Auswerten der Daten nach der Datenaufnahme.
Wer sich näher damit beschäftigt hat wird festgestellt haben, dass das Thema nicht so ganz trivial ist - ganz im Gegenteil.
Nehmen wir also mal an wir haben die Sporen, oder auch andere Elemente richtig vermessen und es liegt eine Messreihe vor.
Wie geht es dann weiter?
Es gibt in der Mykologie verschiedene Arten um Maße darzustellen. Bevor man die selbst aufgenommenen Daten auswertet muss man eigentlich wissen, welche Art der Datenauswertung der Autor der Vergleichsliteratur verwendet hat um entscheiden zu können, welche Methode man selbst für den Literaturvergleich anwenden muss.
Sollte man die "falsche" Methode angewendet haben ist das gar nicht tragisch, so lange man die Messreihe aufbewahrt hat kann man nämlich diese in alle Darstellungsarten umwandeln.
1. die klassische Form der Darstellung von Maßen mit 80% Standardbereich
In den meisten Publikationen werden Sporenmaße (sowie andere Maße von Messreihen) in der –žklassischen Form–œ angegeben.
Jeder hat schon mal diese Darstellung gesehen: [font="Arial"](8.2) 8.9 - 10.3 (10.8) x (4.3) 4.9 - 5.7 (6) µm[/font].
Wenn der Autor nichts angibt oder etwas in der Art "Standardbereich 80%" schreibt - dann handelt es sich in der Regel um diese klassische Darstellung.
Achtung! Wenn der Autor nur so etwas schreibt: [font="Arial"]8.9 - 10.3 x 4.9 - 5.7 µm[/font] - oder noch ungenauer [font="Arial"]9.5 x 5.3 µm[/font], dann hatte er entweder keine Möglichkeiten die Daten zu verarbeiten, kein Wissen, wie man die Daten verarbeitet oder einfach zu weinig Sporen. In diesem Fall ist eigentlich kein richtiger Vergleich möglich, da man gar nicht weiß, was der Autor eigentlich mit der Angabe meint. Das heißt im Umkehrschluss die Angabe ist ungenau oder in machen Fällen sogar unbrauchbar.
Die Vorgehensweise bei der Auswertung:
Bei der –žklassischen Darstellung–œ werden alle Messungen einer Länge zunächst aufsteigend sortiert.
Dann werden 10 –žDezile–œ daraus gebildet, wobei in jedem Dezil ungefähr die gleiche Anzahl an Messwerten ist.
–žUngefähr–œ nur dann wenn die Messwertanzahl nicht durch 10 ganz-zahlig teilbar ist.
Sind Beispielsweise 74 Messungen vorhanden –“ wie im folgenden Beispiel, sind 7 oder 8 Messungen in einem Dezil.
Nun berechnet man zunächst die Dezile wie folgt:
Ein Dezil ist eine Sonderform eines Qunatils.
Ein Quantil ist nichts anderes, als eine Grenze die angibt, wie viele Werte über oder unter einem bestimmten Wert liegen oder - für die Abiturienten unter Euch: Es ist die Umkehrfunktion der kumulativen Verteilungsfunktion.
Es kann also die Aussage daraus getroffen werden:
- im ersten Dezil - also im untersten 10%-Abschnitt befinden sich z.B. 8 Messwerte,
- im ersten und zweiten Dezil - bis zum 20%-Abschnitt befinden sich z.B. insgesamt 15 Messwerte,
usw.
Der Abstand zwischen dem 10%-Dezil und dem 90%-Dezil nennt man Interdezilbereich - und das ist dann in der folgenden Angabe –žmin–œ und –žmax–œ
(kleinster Extremwert) min - max (größter Extremwert)
Der Standardbereich ist also –ž80% breit–œ - unmathematisch aber verständlich ausgedrückt.
Grafisch dargestellt sieht das so aus:
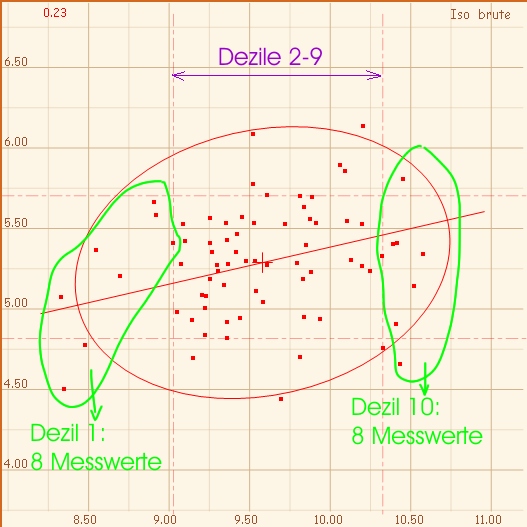
Um nun beispielsweise Grenzwert x für das 10%-Dezil p0,1 (oder die anderen) zu berechnen können wir die allgemeine Quantilformel anwenden:

x1...xn sind die Messwerte
p ist das jeweilige Quantil
n ist die Anzahl der Messwerte
Machen wir das beispielsweise für 74 Messwerte für das 10%-Dezil:
n [font="Times New Roman"] ·[/font] p = 74 x 0,1 = 7,4[font="MS Mincho"] ∉ ℤ[/font]
somit
x[font="Lucida Sans Unicode"]⌈[/font][font="Times New Roman"]n [/font][font="Times New Roman"] ·[/font][font="Times New Roman"] p[/font][font="Lucida Sans Unicode"]⌉=[/font]x[font="Lucida Sans Unicode"]⌈[/font][font="Times New Roman"]74 ·[/font][font="Times New Roman"] 0,1[/font][font="Lucida Sans Unicode"]⌉ = [/font]x[font="Lucida Sans Unicode"]⌈[/font][font="Times New Roman"]7,4[/font][font="Lucida Sans Unicode"]⌉[/font][font="Lucida Sans Unicode"] = [/font]x[font="Times New Roman"]8[/font]
Eine weitere (genauere) Möglichkeit ist das Verfahren der linearen Interpolation mit dem Ansatz:
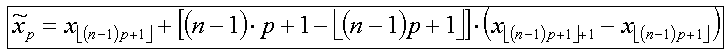
Das heißt es wird noch eine Gerade zwischen 2 Werten gebildet und der Mittelwert interpoliert.
Setzt man für p=0,1 und p=0,9 ein - kann man quasi die min und max-Werte für die Sporenmaßformel direkt berechnen.
Es ist zu erwähnen, dass es noch weitere Quantil-Berechnungsverfahren gibt, die alle etwas unterschiedliche Werte liefern.
Für die Pilzbestimmung ist selbst das ungenaueste genau genug - damit ist nicht weiter von Bedeutung welches Verfahren man verwendet - Hauptsache man verwendet eines.
2. Berechnung des Mittelwertes:
Genau so wichtig ist es, den richtigen Mittelwert zu bestimmen. In der Literatur findet man oft den Begriff "average" oder "mean".
Diese Begriffe bedeuten exakt das gleiche.
Der Mittelwert dieser, wie auch der gleich erklärten Methode ist der arithmetische Mittelwert der Messreihe, also:
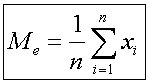
Das war es auch schon.
Oft wird der Mittelwert so dargestellt (unterstrichener Wert)
[font="Times New Roman"](8.2) 8.9 - [/font][font="Times New Roman"]9.5 [/font][font="Times New Roman"]- 10.3 (10.8) x (4.3) 4.9 - [/font][font="Times New Roman"]5.3[/font][font="Times New Roman"] - 5.7 (6) µm[/font]
Bitte beachtet dass der Mittelwert ein genau so wichtiges Bestimmungsmerkmal sein kann wie kleinster Extremwert, min, max und größter Extremwert!
Der arithmetische Mittelwert ist übrigens für alle weiteren Darstellungsformen der "Dimensionsformel" gleich.
Achtung: Oft findet man in der Literatur die Angabe eines Bereiches. Da steht zum Beispiel "average spore width: 5 - 7 µm".
Man könnte hier fehl-interpretieren dass dies ein Standardbereich ist - also z. B. 80% der Sporen 5 - 7 µm breit sind.
Das ist nicht so, sondern "average spore width: 5 - 7 µm" bedeutet dass der arithmetische Mittelwert der Sporenbreite im Bereich 5 - 7 µm liegt.
OK, wir haben also nun schon insgesamt 5 bestimmungsrelevante Werte ermittelt.
Aber es gibt noch viele mehr (wie wir sehen werden).
Wir erkennen schon jetzt...
Aus diesem Wissen ergibt sich, dass eine bestimmte Anzahl an Messungen gemacht werden muss um überhaupt –žmin–œ und –žmax–œ aussagekräftig berechnen zu können.
Ansonsten ist es nicht besonders sinnvoll z.B. die Sporenmaße welche man misst mit Literaturwerten zu vergleichen.
Erb/Matheis geben in Ihrem Buch "Pilzmikroskopie" eine minimale Anzahl von 30 Messungen an (also bei 30 Sporen 30 mal die Länge und 30 mal die Breite = 60 Messwerte).
Dies ist jedoch nur ein grober Richtwert.
Eigentlich ist nämlich die Anzahl der zu messenden Sporen (oder anderer Objekte) von der –žStandardabweichung–œ abhängig –“ was das ist erfahren wir gleich.
Je unterschiedlicher also die Messobjekte (z. B. Sporen) in den Abmessungen sind, umso mehr Sporen muss man messen.
Wie viele Sporen zu messen sind, kann man stochastisch ausrechnen (dazu in einem späteren Bericht mehr, falls es jemand interessiert).
Es ist also nicht sehr sinnvoll, wenn man durch ein Messokular mal hier, mal da eine Spore misst und dann versucht, damit einen aussagekräftigen Vergleich mit Literaturwerten zu machen.
Das bedeutet: Es ist unumgänglich eine Messreihe aufzunehmen und die hier genannten Schritte zu gehen. Daran kommt man nicht vorbei.
Ausnahmen gibt es natürlich, wenn z.B. zu wenig Sporen vorhanden sind, oder wenn man sich mit "cf" einfach mal zufrieden gibt.
Praxisbeispiel von einer unbekannten Hebeloma:
Derzeit bestimme ich mit Matthias eine Hebeloma die sich weigert bestimmt zu werden.
Diese habe ich als Bespiele für diesen Bericht gewählt - was raus kommt zeige ich Euch später in einem anderen Bericht.
Zuerst werden also die Sporen vermessen. Entweder live am Bildschirm, oder anhand der aufgenommenen Bilder oder wie auch immer.
Wie man diese überhaupt richtig misst (Sporenreife, Untersuchungsmedium, Kalibrierung, Aberrationskorrektur, usw., usw.) das soll dieser Bericht nicht beschreiben.
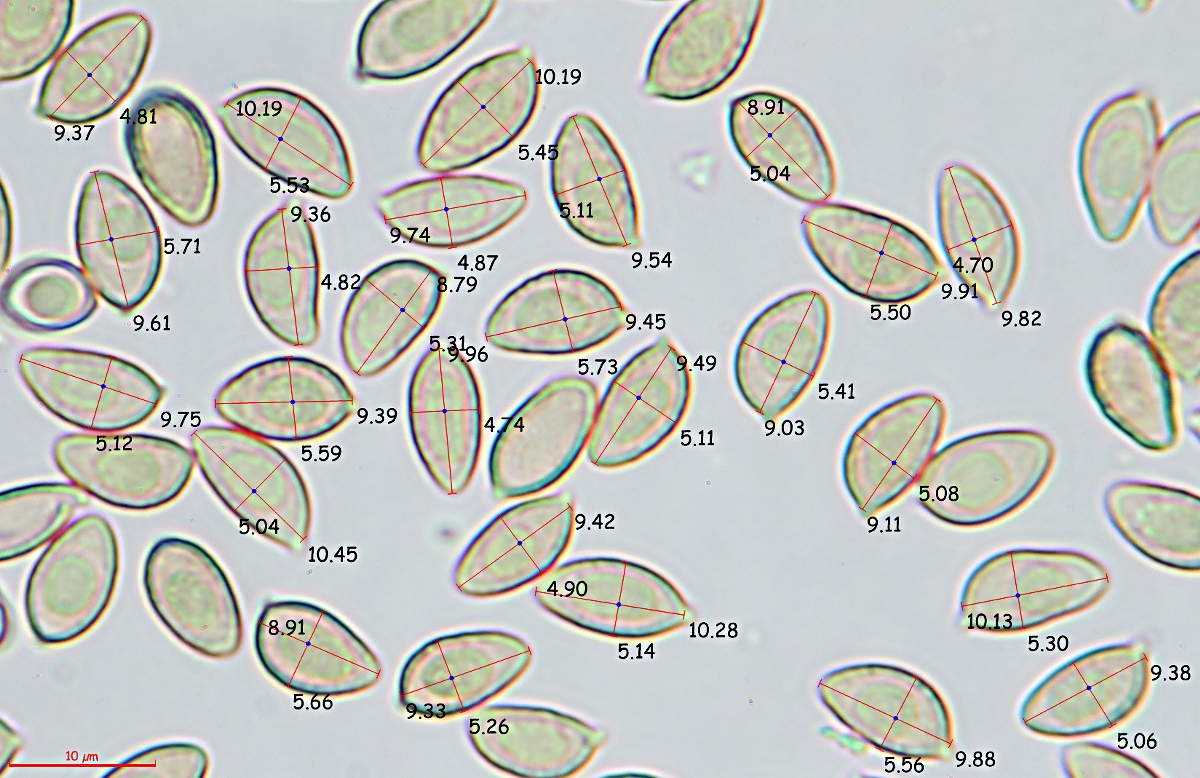
Bei unserer Hebeloma habe ich wegen der nötigen Genauigkeit in diesem schweren Fall 125 Sporen vermessen. Folgende Messwerte nahm ich auf:
8,33 5,08
8,35 4,50
8,48 4,78
8,48 5,57
8,48 5,15
8,55 5,36
8,58 5,21
8,63 5,12
8,65 4,49
8,69 5,20
8,79 5,31
8,86 4,92
8,86 5,61
8,91 5,66
8,91 5,04
8,92 5,41
8,92 5,59
9,03 5,41
9,05 4,98
9,07 5,68
9,07 5,28
9,09 5,53
9,10 5,42
9,11 5,08
9,12 5,19
9,13 5,04
9,13 5,32
9,15 4,93
9,15 4,69
9,18 5,63
9,20 5,09
9,22 4,84
9,23 5,01
9,23 5,08
9,23 5,36
9,25 5,73
9,25 5,57
9,26 5,18
9,26 5,41
9,26 5,36
9,29 4,88
9,29 5,24
9,29 4,53
9,30 5,27
9,31 5,23
9,33 5,26
9,34 5,15
9,35 5,53
9,36 4,82
9,36 5,43
9,36 4,92
9,36 5,28
9,37 4,81
9,38 5,06
9,39 5,59
9,40 5,32
9,41 5,20
9,41 5,35
9,42 4,90
9,42 5,47
9,44 4,95
9,45 5,73
9,45 5,57
9,48 5,30
9,49 5,11
9,52 6,09
9,52 5,78
9,52 5,53
9,53 5,30
9,53 5,30
9,54 5,11
9,54 4,86
9,55 5,06
9,58 5,04
9,61 5,71
9,61 5,27
9,67 5,66
9,67 5,66
9,69 4,44
9,70 5,21
9,72 5,53
9,74 4,87
9,75 5,12
9,80 5,28
9,81 5,70
9,82 4,70
9,82 5,54
9,83 5,18
9,84 5,63
9,84 4,95
9,85 5,40
9,86 5,82
9,87 5,40
9,88 5,56
9,88 5,23
9,88 5,01
9,89 5,70
9,91 5,50
9,92 5,53
9,93 5,17
9,94 4,94
9,96 4,74
9,99 5,58
10,06 5,89
10,09 5,85
10,10 5,55
10,13 5,30
10,19 5,45
10,19 5,53
10,20 5,27
10,20 6,14
10,24 5,23
10,25 5,18
10,28 5,14
10,32 5,46
10,32 5,33
10,33 4,76
10,39 5,40
10,41 4,91
10,42 5,41
10,43 4,66
10,45 5,04
10,45 5,80
10,52 5,14
10,57 5,34
In einem Streudiagramm (Scatter-Plot) mit 95%-Konfidenz-Ellipse und Ursprungsgeraden aufgetragen sieht das so aus:

Die Berechnung von Konfidenz-Ellipsen ist ein komplizierteres Thema - und für uns nicht wirklich wichtig.
Außerdem gibt es unterschiedliche Methoden, und mehrere 95%-Ellipsen die zutreffen.
Aus den sortierten Messwerten berechnet man also zunächst die 10 Dezile. Ich verwende mal zunächst den genauen Ansatz:
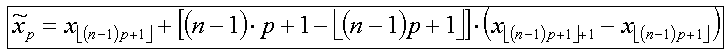
Sowie den arith. Mittelwert mit Ansatz:
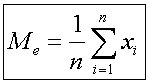
Ergebnis für die LÄNGEN der Sporen:
kleinster Extremwert: 8,33 µm
10%-Dezil: 8,88 µm
20%-Dezil: 9,128 µm
30%-Dezil: 9,26 µm
40%-Dezil: 9,36 µm
50%-Dezil: 9,45 µm
arith. Mittelwert: 9,51728 µm
60%-Dezil: 9,61 µm
70%-Dezil: 9,828 µm
80%-Dezil: 9,932 µm
90%-Dezil: 10,246 µm
Größter Extremwert: 10,57 µm
Nur die roten Werte sind für uns interessant und man kann diese sofort in die Form bringen:
[font="Arial"]Sporenlänge: (8.33) 8.88 - 9.51728 [/font][font="Times New Roman"][font="Arial"]- 10.246 (10.57) µm[/font]
[/font]
Mit dem Ansatz:

welchen ich üblicher Weise verwende kommt man übrigens auf:
10%-Dezil: 8,86 µm
90%-Dezil: 10,25 µm
Diese geringe Abweichung ist für uns Schwammerfreunde wirklich kein Problem, und nach der Rundung ist davon sowieso nichts mehr zu erkennen.
Das gleiche tun wir für die Breiten - und es ergibt sich die "Dimensionsformel" - gültig für die klassische 80%-Darstellung:
Sporenlänge × Sporenbreite: (8,33) 8,88 - 9,52 - 10,246 (10,57) × (4,44) 4,848 - 5,27 - 5,672 (6,14) µm
Dies ist die best mögliche Auswertung der Daten. Diese Berechnungsmethode verwende ich normalerweise für die Daten in meinen Berichten hier.
Auch wenn es am Anfang kompliziert erscheinen mag - natürlich dauert das ganze bei mir nur wenige Minuten - da alles bereits per CASB (= Computer Aided Schwammer Bestimmung) automatisiert ist.  Genau so wie folgende Berechnungsergebnisse automatisch immer mit ausgespuckt werden.
Genau so wie folgende Berechnungsergebnisse automatisch immer mit ausgespuckt werden.
Das gleiche können wir auch für Q, B/L und V machen. Q ist wie Ihr sicher wisst das Länge- zu Breite-Verhältnis.
B/L ist der Kehrwert von Q, also 1/Q. V ist das geschätzte Sporenvolumen - wie man das berechnet seht ihr weiter unten.
Ich tue das für den Beispiel-Pilz. Ergebnis - komplett und in schöne gerundete Form gebracht:
arith. Mittelwert Me L × B: 9,52 × 5,27 µm
arith. Mittelwert Me Q: 1,81
arith. Mittelwert Me B/L: 0,555
arith. Mittelwert Me V: 139 µm ³
und dazu einmal alle Dimensionsformeln klassische Darstellung mit 80%-Standardbereich:
L × B für 80% CR: (8,33) 8,88 - 10,25 (10,57) × (4,44) 4,85 - 5,67 (6,14) µm
Q für 80% CR: (1,52) 1,65 - 1,98 (2,24)
B/L für 80% CR: (0,447) 0,504 - 0,607 (0,657)
V für 80% CR: (89) 116 - 163 (201) µm ³
3. die klassische Form der Darstellung von Maßen mit 90% Standardbereich
In der modernen Pilzliteratur gibt es inzwischen eine weitere Darstellungsart der Dimensionsformeln.
Zum Beispiel in der aktuellsten Hebeloma-Monografie (Fungi Europaei 14 von Baker, Eberhardt & Vesterholt 2016) sind die Sporenwerte sowie alle anderen Messwerte nämlich grundsätzlich nur in der 90%-Darstellung auf klassische Art berechnet und angegeben. Dort ist zu lesen "(min) 5% - 95% (max)".
Wer dieses Werk nicht hat kann aber auch in Persoonia Volume 35 (Dezember 2015) - Seite 111 - "Decrypting the Hebeloma crustuliniforme complex: European species of Hebeloma section Denudata subsection Denudata (Agaricales)" nachlesen.
EDIT: Auch Funga Nordica verwendet den 90% Standardbereich und die klassische Dimensionsformeldarstellung.
Der Grund dafür war mir zunächst rätselhaft, bis ich las, dass die Autorem mit der Leica-Auswertungssoftware "QWIN" arbeiteten die eben diesen Standardbereich (vermutlich standardmäßig) auswirft und in eine Datenbank schreibt. Mit ein paar Handgriffen musste ich also meine eigenen Auswertungsroutinen und mein Ausgabeblatt um ein paar Formeln ergänzen.
Wie berechnet man diesen 90%-Standardbereich?
Die Vorgehensweise ist genau gleich wie beim 80%-Standardbereich, nur dass man die Messreihe nicht in 10 Dezile unterteilt sondern in 20 je 5% breite Perzentile.
Der Standardbereich ist also nun –ž90% breit–œ (90%, weil 95% minus 5 % = 90%).
Wir setzen also in unsere oben genannten Formeln:

oder
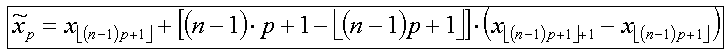
für das 5%-Perzentil p = 0,05 ein, und für das 95%-Perzentil p = 0,95.
Ich mache das für unsere Messwertreihe oben für die Längen und bekomme folgende Ergebnisse:
kleinster Extremwert: 8,33 µm
5%-Perzentil: 8,59 µm
arith. Mittelwert: 9,52 µm
95%-Perzentil: 10,406 µm
Größter Extremwert: 10,57 µm
Kleinster Extremwert, arith. Mittelwert und größter Extremwert sind logischer Weise wieder die gleichen.
Das gleiche mache ich für die Breiten und erhalte die Dimensionsformel für den 90%-Standardbereich:
(8,33) 8,59 - 9,52 - 10,406 (10,57) × (4,44) 4,708 - 5,27 - 5,770 (6,14) µm
Vergleichen wir diese doch einmal mit der Dimensionsformel der 80%-Standardbereich-Darstellung:
(8,33) 8,88 - 9,52 - 10,246 (10,57) × (4,44) 4,848 - 5,27 - 5,672 (6,14) µm
Wir erkennen den Unterschied (rote Werte) deutlich. Nun könnte man sagen - "naja macht nicht viel aus" - bei anderen Elementen - z.B. Cheilozystidenlängen macht das eben schon was aus.
Man muss also hier, sowie in anderer Literatur genau aufpassen was man eigentlich vergleicht.
Es wäre - speziell bei Hebeloma fatal, mit dem anderen Verfahren als angegeben die Werte zu ermitteln und dann in einem Schlüssel versuchen damit weiter zu kommen.
In den Schlüsseln sind die Schlüsselpunkte so sehr fein unterteilt, dass kleinste Fehler im Mess- und Berechnungsverfahren in einigen Fällen schon zu einer Fehlbestimmung führen würde.
Aber es gibt noch weitere Formen der Darstellung von Dimensionsformeln - kommen wir nun aber zunächst zu einen anderen wichtigen Wert, den wir kennen müssen um diese anderen Darstellungsarten zu verstehen.
Das gleiche können wir auch für Q, B/L und V machen.
Ich tue das für den Beispiel-Pilz. Ergebnis - komplett und in schöne gerundete Form gebracht:
Alle Dimensionsformeln klassische Darstellung mit 90%-Standardbereich:
L × B für 90% CR: (8,33) 8,59 - 10,41 (10,57) × (4,44) 4,71 - 5,77 (6,14) µm
Q für 90% CR: (1,52) 1,6 - 2,07 (2,24)
B/L für 90% CR: (0,447) 0,483 - 0,625 (0,657)
V für 90% CR: (89) 112 - 168 (201) µm ³
4. Die Standardabweichung:
Ein bestimmungsrelevantes Merkmal von Pilzen ist die "Standardabweichung" von Sporenmaßen und anderen mikroskopischen Elementen.
In der Literatur findet man die Angaben "S. D." für Standard deviation = Standardabweichung oder σ (sprich: Sigma).
Bestimmungstechnisch sinnvoll ist die Ermittlung natürlich nur dann, wenn Vergleichswerte für diese überhaupt vorliegen, das heißt von jemandem einmal festgestellt wurden.
Bei unserer Bespiel-Hebeloma ist dies garantiert der Fall. Die Standardabweichung - ganz einfach erklärt - gibt an, wie groß die Wahrscheinlichkeit ist, dass eine gemessene Größe vom Erwartungswert abweicht.
Sind zum Beispiel Sporenlängen stark unterschiedlich, haben Sie eine hohe Standardabweichung.
Genau dies wird in professioneller Literatur ausgewertet und als Merkmal angegeben.
Die Längenverteilung von Sporen folgt oft der Gauß'schen Normalverteilung - jedoch nicht immer oder oft nur annähernd.
Um das zu verdeutlichen habe ich einmal die Längen der Beispiel-Sporen in 9 "Bins" (Quantile) verteilt und die Häufigkeit über die Sporenlänge geplottet und die Gaussche Normalverteilung mit
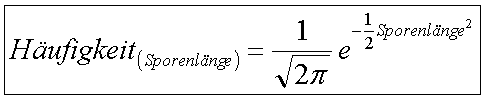
darüber gelegt:
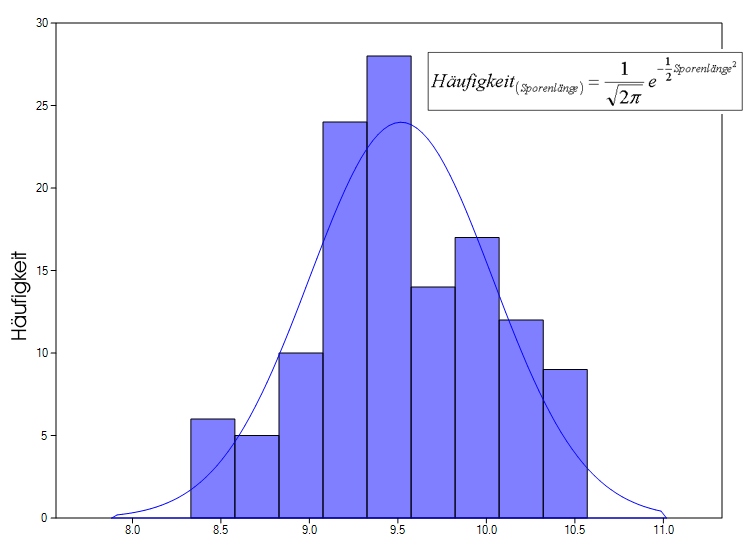
Man erkennt die Formabweichung deutlich.
Wie berechnen wir aber nun diese Standardabweichung?
Bei der Normalverteilung befinden sich immer 68,2689492% der Messwerte im Intervall der Breite von 2 Standardabweichungen (2 × σ) um den Erwartungswert (Me).
Der Erwartungswert ist nichts anderes als der oben berechnete arithmetische Mittelwert.
σ berechnen wir über die Gleichung:
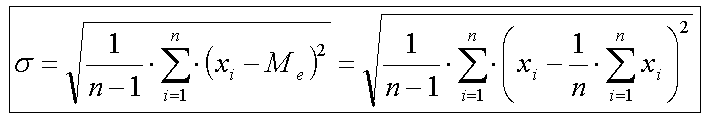
σ ist die Standardabweichung
x1...xn sind die Messwerte
n ist die Anzahl der Messwerte
Me ist der arithmetische Mittelwert der Messreihe
Für unseren Beispielpilz habe ich das gemacht. Hier das Ergebnis:
σ der Sporenlänge: 0,5172 µm
σ der Sporenbreite: 0,3328 µm
Anders geschrieben: σxy = 0,5172 × 0,3328 µm
Was sagt uns das nun?
Es sagt uns:
"Der Erwartungswert der Sporenlänge ist 9,52 µm und bei 68% der gemessenen Sporen wird die gemessene Länge innerhalb der Standardabweichung also innerhalb 9,52 µm ± 0,5172 µm also zwischen 9 und 10,03 µm liegen.
Der Erwartungswert der Sporenbreite ist 5,27 µm und bei 68% der gemessenen Sporen wird die gemessene Länge innerhalb der Standardabweichung also innerhalb 5,27 µm ± 0,3328 µm also zwischen 4,94 und 5,6 µm liegen."
Na das ist doch gut zu wissen, stimmt's? 
Auch hier hoffe ich die Fragen zu dem von mir manchmal benutzten "Sigma" beantwortet zu haben.
Das gleiche können wir auch für Q, B/L und V machen.
Ich tue das für den Beispiel-Pilz. Ergebnis - komplett und in schöne gerundete Form gebracht:
Alle Standardabweichungen sind:
Standardabweichung S. D. von L × B: 0,52 × 0,33 µm
Standardabweichung S. D. von Q: 0,14
Standardabweichung S. D. von B/L: 0,042
Standardabweichung S. D. von V: 20 µm ³
5. Die statistische Form der Darstellung von Dimensionsformeln
Mit diesem Wissen von Standardabweichung und σ werden wir nun bald auch die Darstellung wie folgt verstehen:
Manchmal sieh man eine solche Darstellung:
9.00 [9.47 ; 9.56] 10.03 x 4.94 [5.24 ; 5.30] 5.60 µm ; C = 68%
oder:
8.50 [9.43 ; 9.61] 10.53 x 4.62 [5.21 ; 5.33] 5.92 µm ; C = 95%
Diese Dimensionsformeln sind übrigens exakt von der oben genannten Messreihe berechnet.
Wir erkennen: Es gibt hier keinen kleinsten Extremwert und keinen größten Extremwert mehr.
C steht für Confidence Range, das so genannte "Vertrauensbereich".
Die Werte in dieser Darstellung sagen etwas völlig anderes aus als bei der klassischen Darstellung.
Min [m ; M] Max bedeuten wenn C = 95% folgendes (für C = 68% bitte 68% einsetzten):
a) Es besteht eine Wahrscheinlichkeit von 95% dass der Messwert (z. B. Sporenlänge) im Bereich von Min bis Max liegt. Und,
b) es besteht eine Wahrscheinlichkeit von 95% dass das Intervall [m bis M] den arithmetischen Mittelwert der Messreihe enthält.
Was soll das?
Erinnern wir uns an die Standardabweichung:
"Bei der Normalverteilung befinden sich immer 68,2689492% der Messwerte im Intervall der Breite von 2 Standardabweichungen (2 × σ) um den Erwartungswert (Me)."
Das heißt, dass wenn C = (ca.) 68%, der Vertrauensbereich also 2 Standardabweichungen breit ist.
Genau so bedeutet es, dass wenn C = (ca.) 95% der Vertrauensbereich also 4 Standardabweichungen breit ist.
Und nun wissen wir sofort wie wir die Werte dieser Dimensionsformel berechnen.
Für Min und Max müssen wir logischer Weise nur den arithmetischen Mittelwert ±Ïƒ (für C = 68%) bzw. ±2σ (für C = 95%) rechnen.
Die Formeln dafür sind also:

m und M berechnen wir so:
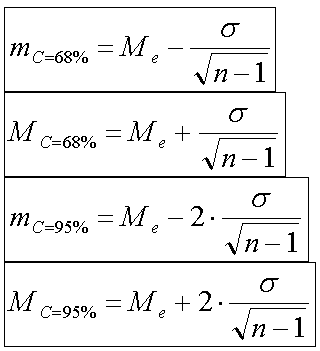
Das war's schon - probiert es gleich mal aus.
Das gleiche können wir auch für Q, B/L und V machen.
Ich tue das für den Beispiel-Pilz. Ergebnis - komplett und in schöne gerundete Form gebracht:
Alle Dimensionsformeln statistische Darstellung mit 68%-Vertrauensbereich:
L × B für 68% CR: 9 [9,47; 9,56] 10,03 × 4,94 [5,24; 5,3] 5,6 µm
Q für 68% CR: 1,67 [1,8; 1,83] 1,95
B/L für 68% CR: 0,513 [0,551; 0,559] 0,597
V für 68% CR: 119 [137; 141] 159 µm ³
Alle Dimensionsformeln statistische Darstellung mit 95%-Vertrauensbereich:
L × B für 95% CR: 8,5 [9,43; 9,61] 10,53 × 4,62 [5,21; 5,33] 5,92 µm
Q für 95% CR: 1,54 [1,79; 1,84] 2,09
B/L für 95% CR: 0,473 [0,548; 0,562] 0,637
V für 95% CR: 100 [135; 143] 179 µm ³
6. Die Mediane
Es gibt noch mehr bestimmungsrelevante Messgrößen von Pilzteilen. Der Median ist eine nicht so bekannte.
Die oben genannte Pilzliteratur verwendet Mediane, sogar Median-Bereiche.
Der Median wird auch "Zentralwert" genannt und ist ein Mittelwert in der Statistik, jedoch nicht der arithmetische Mittelwert.
Der Median teilt eine Messreihe in 2 Hälften. Auch hier muss die Messreihe wieder aufsteigend sortiert werden vor der Berechnung.
Eben weil er in der Mitte der Messreihe liegt berechnet er sich logischer Wiese wie folgt:
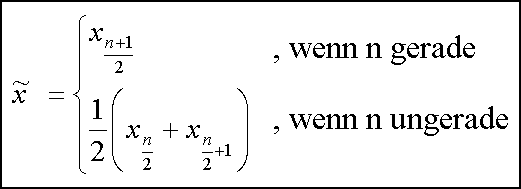
Ich habe das für unsere Beispiel-Hebeloma gemacht. Ergebnis:
Median der Sporenlänge: 9,45 µm
Median der Sporenbreite: 8,25 µm
Vergleichen wir das mit dem arithmetischen Mittelwert:
Arithmetischen Mittelwert der Sporenlänge: 9,52 µm
Arithmetischen Mittelwert der Sporenbreite: 5,27 µm
Wir sehen den Unterschied... aber wozu soll das gut sein?
Der Median hat einen Vorteil in der Statistik, er ist unempfindlich gegen Ausreißer. Stellt Euch mal vor es gibt eine Riesenspore in einer kleinen Messreihe mit wenig Werten.
Was passiert? Der Median ändert sich kaum, der arithmetische Mittelwert jedoch schießt in die Höhe.
Die Bestimmung von Medianen hat also durchaus seine Berechtigung. Ich mache das immer, alleine zu Bestätigung des arithmetischen Mittelwertes.
Das gleiche können wir auch für Q, B/L und V machen.
Ich tue das für den Beispiel-Pilz. Ergebnis - komplett und in schöne gerundete Form gebracht:
Alle Mediane sind:
Median von L × B: 9,45 × 5,28 µm
Median von Q: 1,8
Median von B/L: 0,555
Median von V: 139 µm ³
7. Das geschätzte Sporenvolumen
Das ungefähre Volumen - abgeleitet aus den Rotationsellipsoid-Gleichungen ist:
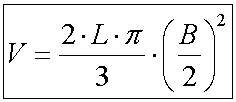
Alle Volumenwerte im Überblick für unsere Beispiel-Hebeloma berechnet sehen so aus:
Arith. Mittelwert Me von V: 139 µm ³
Standardabweichung S. D. von V: 20 µm ³
Median von V: 139 µm ³
V für 80% CR: (89) 116 - 163 (201) µm ³
V für 90% CR: (89) 112 - 168 (201) µm ³
V für 68% CR: 119 [137; 141] 159 µm ³
V für 95% CR: 100 [135; 143] 179 µm ³
8. Mein Ausgabeblatt einer Messung
Das vollständige numerische Ausgabeblatt - welches ich Euch noch nie gezeigt habe schaut bei mir also so aus:
Ermittelte Dimensionswerte allgemeingültig:
Messwertanzahl: n = 125
arith. Mittelwert Me von L × B: 9,52 × 5,27 µm
arith. Mittelwert Me von Q: 1,81
arith. Mittelwert Me von B/L: 0,555
arith. Mittelwert Me von V: 139 µm ³
Standardabweichung S. D. von L × B: 0,52 × 0,33 µm
Standardabweichung S. D. von Q: 0,14
Standardabweichung S. D. von B/L: 0,042
Standardabweichung S. D. von V: 20 µm ³
Median von L × B: 9,45 × 5,28 µm
Median von Q: 1,8
Median von B/L: 0,555
Median von V: 139 µm ³
Dimensionsformeln klassische Darstellung mit 80%-Standardbereich:
L × B für 80% CR: (8,33) 8,88 - 10,25 (10,57) × (4,44) 4,85 - 5,67 (6,14) µm
Q für 80% CR: (1,52) 1,65 - 1,98 (2,24)
B/L für 80% CR: (0,447) 0,504 - 0,607 (0,657)
V für 80% CR: (89) 116 - 163 (201) µm ³
Dimensionsformeln klassische Darstellung mit 90%-Standardbereich:
L × B für 90% CR: (8,33) 8,59 - 10,41 (10,57) × (4,44) 4,71 - 5,77 (6,14) µm
Q für 90% CR: (1,52) 1,6 - 2,07 (2,24)
B/L für 90% CR: (0,447) 0,483 - 0,625 (0,657)
V für 90% CR: (89) 112 - 168 (201) µm ³
Dimensionsformeln statistische Darstellung mit 68%-Vertrauensbereich:
L × B für 68% CR: 9 [9,47; 9,56] 10,03 × 4,94 [5,24; 5,3] 5,6 µm
Q für 68% CR: 1,67 [1,8; 1,83] 1,95
B/L für 68% CR: 0,513 [0,551; 0,559] 0,597
V für 68% CR: 119 [137; 141] 159 µm ³
Dimensionsformeln statistische Darstellung mit 95%-Vertrauensbereich:
L × B für 95% CR: 8,5 [9,43; 9,61] 10,53 × 4,62 [5,21; 5,33] 5,92 µm
Q für 95% CR: 1,54 [1,79; 1,84] 2,09
B/L für 95% CR: 0,473 [0,548; 0,562] 0,637
V für 95% CR: 100 [135; 143] 179 µm ³
Ich hoffe nun seid Ihr nicht erschlagen von den ganzen Zahlen zu nur einer einzigen Sporenmessung 
9. Was noch?
Wer nun denkt "Das müssen aber doch nun alle Werte sein die man aus einer Sporenmessreihe ermitteln kann" der irrt.
Es gibt noch mehr.
Beispiele:
- die "Varianz" - bei unserer Beispiel Hebeloma übrigens 0,26756 µm für die Länge und 0,11075 für die Breite.
- "Testen auf Normalverteilung" mit den entsprechenden Ergebnissen. Hier einmal 3 Stück dargestellt für die Sporenlänge:
Shapiro-Wilk W 0,9833
p(normal) 0,1267
Anderson-Darling A 0,5099
p(normal) 0,1938
p(Monte Carlo) 0,1989
Jarque-Bera JB 1,109
p(normal) 0,5742
p(Monte Carlo) 0,5305
usw usw...  Nun alles klar? Na dann viel Spaß beim Nachmachen...
Nun alles klar? Na dann viel Spaß beim Nachmachen...
Genug Theorie - Ran ans Mikroskop und viel Spaß beim Rechnen!
Ich freue mich Über Eure Kommentare, Verbesserungsvorschläge, Tipps, etc.
Beste Grüße
Dieter


